Question

Find the 55th term in the following arithmetic sequence: -102, -98,-94, -90, ...

Answer 1

We are given the following sequence:

`-102,-98,-94,-90`

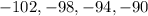
This is an arithmetic sequence that means that each term can be found by adding a constant term to the previous term. In this case, that constant term is 4, since:

`\begin{gathered} -102+4=-98 \\ -98+4=-94 \\ -94+4=-90 \end{gathered}`

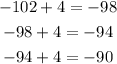
This term is called the common difference. The n-th term of an arithmetic sequence is given by:

`a_n=a_1+(n-1)d`

Where:

`\begin{gathered} a_1=\text{first term} \\ d=\text{common difference} \end{gathered}`

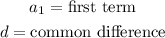
In this case, we have:

`a_n=-102+(n-1)4`

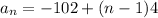
Solving the operations we get:

`a_n=-102+4n-4`

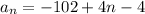
Simplifying:

`a_n=-106+4n`

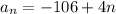
Now we replace "n = 55" since we want to find the 55th term:

`a_(55)=-106+4(55)`

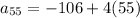
Solving the operations:

`a_(55)=114`

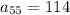
Therefore the 55th term is 114