Question

Lookout station A is 12 miles from the fire. Lookout station B is 39 miles from station A. The angle at station A is 52°. Find the distance between Station B and the fire.

Answer 1

I might be A is 52 hopefully its correct

Answer 2

Therefore, in order to find out the distance from station b to the fire, we must use the sine formula, as we know that sine is the opposite side divided by the hypotenuse.

We want to find out the opposite side and we already have the hypotenuse that is 12 miles.

So:

`\begin{gathered} \sin52=\text{ }(x)/(12) \\ 12(\sin52)=x \\ 12(0.788)=x \\ 9.456=x \end{gathered}`

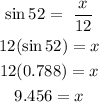
Therefore, station B i 09.456 miles from the fire.