Question

The vertices of quadrilateral DEFG are D(-2, 6), E(-4, 6), F(-6, 9), and G(-1,9). Find the coordinates of the image of quadrilateral DEFG after a translation using the rule (x,y) - (x + 1. y - 6), a reflection over the x-axis, and a reflection over the y-axis.

Answer 1

We have the following quatrilateral DEFG:

We will do various transformations to it.

1. Traslation (x+1,y-6)

For doing this traslation, we will apply the formula to each one of the endpoints of the quadrilateral. For the sake of this exercise, we will call the traslation T.

`\begin{gathered} D^(\prime)=T(D)=T(-2,6) \\ =(-2+1,6-6) \\ =(-1,0) \end{gathered}`

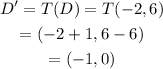
Where we obtained the coordinates values by replacing the x-coordinate of the point A by the value x of the traslation, and doing the same process for the y-coordinate. We obtain also,

`\begin{gathered} E^(\prime)=T(E)=T(-4,6) \\ =(-4+1,6-6) \\ =(-3,0) \end{gathered}`

For F,

`\begin{gathered} F^(\prime)=T(F)=T(-6,9) \\ =(-6+1,9-6) \\ =(-5,3) \end{gathered}`

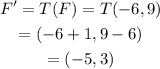
For G, following the same process we obtain that G'=T(G)=(0,3). This gives us the quadrilateral:

2. Reflection over the x-axis

For doing a reflection over the x-axis, we will follow the rule:

`R_x\lbrack x,y\rbrack=(x,-y)`

In this case, we will apply the rule to every endpoint of the quadrilateral.

`\begin{gathered} D^(\prime)=R_x\lbrack D\rbrack=R_x(-2,6)=(-2,-6) \\ E^(\prime)=R_x\lbrack E\rbrack=R_x(-4,6)=(-4,-6) \\ F^(\prime)=R_x\lbrack F\rbrack=R_x(-6,9)=(-6,-9) \\ G^(\prime)=R_x\lbrack G\rbrack=R_x(-1,9)=(-1,-9) \end{gathered}`

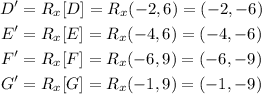
3. Reflection over the y-axis

For doing a reflection over the y-axis, we will follow the rule:

`R_y\lbrack(x,y)\rbrack=(-x,y)`

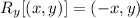
And we apply the rule to every endpoint of the quadrilateral.

`\begin{gathered} D^(\prime)=R_y\lbrack D\rbrack=R_y(-2,6)=(2,6) \\ E^(\prime)=R_y\lbrack E\rbrack=R_y(-4,6)=(4,6) \\ F^(\prime)=R_y\lbrack F\rbrack=R_y(-6,9)=(6,9) \\ G^(\prime)=R_y\lbrack G\rbrack=R_y(-1,9)=(1,9) \end{gathered}`

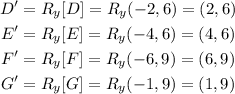
We obtain the quadrilaterals: