Question

Determine whether WX and YZ are parallel, perpendicular or neither.W(6.-6), X(7.1). Y(3,-1), Z(2,6)

Answer 1

Neither

Step-by-step explanation

To determine whether WX and YZ are parallel or perpendicular, wehave to find their slopes and compare them.

Slope is given as:

`\text{slope = }\frac{y_2-y_1}{x_{2_{}}-x_1}`

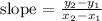
SLOPE OF WX

For WX,

(x1, y1) = (6, -6)

(x2, y2) =(7, 1)

So:

`\begin{gathered} \text{slope = }\frac{1\text{ - (-6)}}{7\text{ - 6}}\text{ = }\frac{1\text{ + 6}}{1} \\ \text{slope = 7} \end{gathered}`

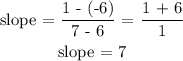
SLOPE OF YZ

For YZ:

(x1, y1) = (3, -1)

(x2, y2) = (2, 6)

So:

`\begin{gathered} \text{slope = }\frac{6\text{ - (-1)}}{2\text{ - 3}} \\ \text{slope = }\frac{6\text{ + 1}}{-1} \\ \text{slope = -7} \end{gathered}`

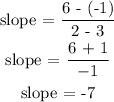
For WX and YZ to be parallel, their slope must be the same.

For WX and YZ to be perpendicular, the slope of one must be the negative inverse of the other.

Since their slopes are neither the same or the negative inverse of one another, WX and YX are neither parallel or perpendicular to one another.