Given data
Height = 16.8 ft
Slant height = 19.3 ft
First, you find the base of the right angle triangle in the daigram.
Opposite = 16.8 ft
Hypotenuse = 19.3 ft
Adjacent = b
![\begin{gathered} \text{Appy pythagorus theorem} \\ \text{Opp}^2+Adj^2=Hypotenuse^2 \\ 16.8^2+b^2=19.3^2 \\ 282.24+b^2\text{ = 372.49} \\ b^2=372.49\text{ - 282.24} \\ b^2\text{ = 90.25} \\ b\text{ = }\sqrt[\square]{90.25} \\ b\text{ = 9.5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ot1ffjyqgpbmx9c52ynkdyxs8whpb2e1rh.png)
Next,
The side of the base of the pyramid = 2 x b
= 2 x 9.5
= 19
The square measure 19 ft
To find the surface area of the pyramid, sum the areas of the square base and the area of the four triangles.
Area of the square = 19 x 19 = 361
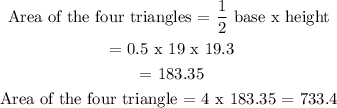
Toal surface area of the figure = 733.4 + 361
= 1094.4