Question

Can you solve 11???? and go in depth on how to do it

Answer 1

Given the Right Triangle (because it has an angle that measures 90 degrees) shown in exercise 11, you know an interior angle that measures 60 degrees and a side whose length is 13 centimeters.

• By definition, the sum of the interior angles of a triangle is 180 degrees. Then, in order to find the third angle, you can set up this equation:

`m\angle A=180\degree-90\degree-60\degree`

Where "A" is the missing angle.

Simplifying, you get:

`m\angle A=30\degree`

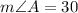
• To find the hypotenuse of the triangle, you need to apply this Trigonometric Function:

`\cos \beta=(adjacent)/(hypotenuse)`

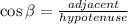
In this case:

`\begin{gathered} \beta=60\degree \\ adjacent=13 \\ hypotenuse=c \end{gathered}`

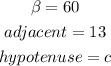
Let be "c" the length (in centimeters) of the hypotenuse of the Right Triangle.

Substituting values and solving for "c", you get:

`\begin{gathered} \cos (60\degree)=(13)/(c) \\ \\ c\cdot\cos (60\degree)=13 \\ \\ c=(13)/(\cos (60\degree)) \\ \\ c=26 \end{gathered}`

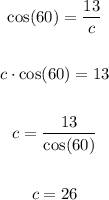
• In order to find the length of the missing leg of the triangle, you can apply the Pythagorean Theorem, which states that:

`c^2=a^2+b^2`

Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.

Leg be "a" the length (in centimeters) of the missing leg.

Knowing the hypotenuse and the length of the other leg, you can substitute values and solve for "a":

`\begin{gathered} 26^2=a^2+13^2 \\ 26^2-13^2=a^2 \\ \sqrt[]{26^2-13^2}=a \\ a=13\sqrt[]{3}^{} \end{gathered}`

Hence, the answer is: