We have two statements, and each one of them gives us a different equation. We want to find out two numbers. Let's call them 'x' and 'y'. "State the factor pair of 144", this means the product between those numbers is equal to 144.
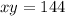
"that has a difference of 10" and this means that the difference between them is 10. Let's assume x < y.
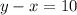
Now, we have two equations with two variables.
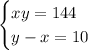
Let's rewrite 'x' as a function of 'y' in the first equation, and then, substitute in the second one.
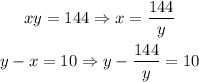
Solving the second equation for 'y', we have:
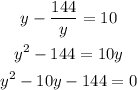
Using the bhaskara equation to get the roots, we have the following possible values for 'y':
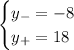
If we use the negative root, we have:
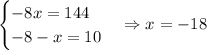
If we use the positive root:

-18 and -8, or 8 and 18, both fits the answer. Since we're talking about factor pairs, it makes sense to consider only the positive pair, 8 and 18.