The box has 3 white balls and 4 black balls.
Total number of balls = 3 + 4 = 7
First draw:
The probability of getting a white ball is given by
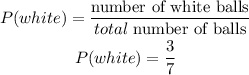
Second draw:
Notice that after the first draw the ball is put back in the box.
The probability of getting a white ball is given by
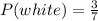
At least one of the balls is white means that one white ball or two white balls.
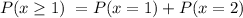
We have already found the probability of getting one white ball that is P(x=1) = 3/7
The probability of getting two white balls is
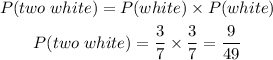
Finally, the probability of at least one white ball is

Therefore, the probability of the event that at least one of the balls is white is 30/49