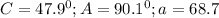Question

Consider a triangle ABC like the one below. Suppose that b=46, c=51, andB=42°. (The figure is not drawn to scale.) Solve the triangle.Carry your intermediate computations to at least four decimal places,and round your answers to the nearest tenth.If no such triangle exists, enter "No solution." If there is more than onesolution, use the button labeled "or".

Answer 1

Explanation

The first step is to recreate the triangle using the given values.

We can find the value of angle C using the sine rule below.

`\frac{\text{SinB}}{b}=\frac{\text{SinC}}{c}`

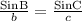
We insert the necessary parameters.

`\begin{gathered} (Sin42)/(46)=\frac{\text{SinC}}{51} \\ Crossmultiply \\ 46SinC=Sin42*51 \\ SinC=(Sin42*51)/(46) \\ C=\sin ^(-1)0.7419 \\ C=47.9^0 \end{gathered}`

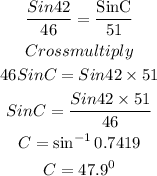
We can find the value of A using the sum of angles in a triangle.

`\begin{gathered} A+B+C=180 \\ A+42+47.9=180 \\ A=180-42-47.9 \\ A=90.1 \end{gathered}`

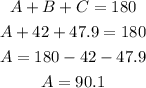
We can find the side "a" using the cosine rule

`\begin{gathered} a^2=b^2+c^2-2\text{bc}* CosA \\ a^2=46^2+51^2-2*46*51\text{Cos}90.1 \\ a^2=2116+2601+8.1891 \\ a^2=4725.1891 \\ a^{}=\sqrt[]{4725.1891} \\ a=68.7 \end{gathered}`

Answer:

`C=47.9^0;A=90.1^0;a=68.7`