Question

The demand for a kayak for $700 is 80 kayaks and $400 is 175 kayaks at Pepito's kayaks stores. Assume that the demand function in linear.a. Find the demand function (5point)b. What is the demand for 600? (5 point)

Answer 1

Given

`\begin{gathered} \text{When price is \$700, kayaks is 80, and} \\ \text{When price is \$400, kayaks is 175} \end{gathered}`

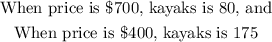
If the price represents the dependent variable y and the number of kayaks represents the independent variable x, then we can represent the given information as

`\begin{gathered} y_1=700,x_1=80 \\ y_2=400,x_2=175 \end{gathered}`

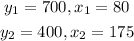
Assuming that the demand function is linear. Then we can determine the function using the general equation of a linear function formula with two different points.

The formula for finding the function of a linear function with two points is

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

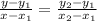
Substituting the given points

`\begin{gathered} (y-700)/(x-80)=(400-700)/(175-80) \\ (y-700)/(x-80)=(-300)/(95) \end{gathered}`

`\begin{gathered} (y-700)/(x-80)=(-60)/(19) \\ \text{cross}-\text{multiyiply} \\ 19(y-700)=-60(x-80) \end{gathered}`

`\begin{gathered} 19y-13300=-60x+4800 \\ 19y=-60x+4800+13300 \\ 19y=-60x+18100 \\ y=-(60)/(19)x+(18100)/(19) \end{gathered}`

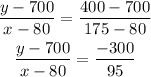
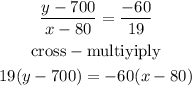
When y is 600, x would be

`\begin{gathered} 600=-(60)/(19)x+(18100)/(19) \\ \text{mltiply through by 19} \\ 19*600=-60x+18100 \\ 11400=-60x+18100 \\ 11400+60x=18100 \end{gathered}`

`\begin{gathered} 60x=18100-11400 \\ 60x=6700 \\ x=(6700)/(60) \end{gathered}`

`\begin{gathered} x=111.67 \\ x\approx112 \end{gathered}`

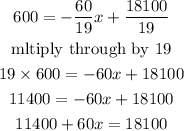
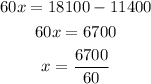
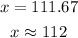
Answer Summary

(a) The demand function is y= -60/19x +18100/19, or 19y=-60x+18100

(b) The demand for $600 is approximately 112 kayaks