Given:
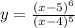
To Determine: Where the tangent line is horizontal
Solution
Please note where the tangent line is horizontal is when the derivative is equal to zero
Determine the derivative of the function using quotient rule
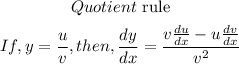
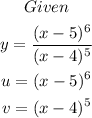
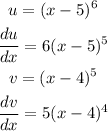
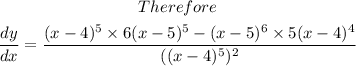
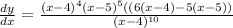
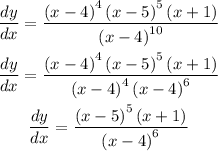
Equate the derivative to zero
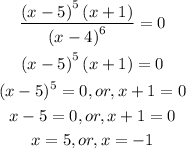
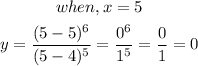
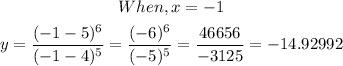
Hence
(5,0) and (-1,-14.92992)
x=(-1, 5)