Question

Solve the following systems of equations algebraically. If there are no real solutions, type “none” in both blanks. If there is only one, type “none” in the other blank.

Answer 1

Answer: We have to find the algebraic solution for the system of equations:

`\begin{gathered} y=-2x-4\Rightarrow(1) \\ \\ y=x^2+6x+8\Rightarrow(2) \end{gathered}`

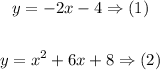
The solution is simply a point where (1) and (2) have the same coordinates, which basically means that we have to set two equations equal, therefore the solution is as follows:

`\begin{gathered} (1)=(2) \\ \\ -2x-4=x^2+6x+8 \\ \\ x^2+8x+12=0\Rightarrow(3) \end{gathered}`
`\begin{gathered} (1)=(2) \\ \\ -2x-4=x^2+6x+8 \\ \\ x^2+8x+12=0\Rightarrow(3) \end{gathered}`

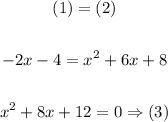
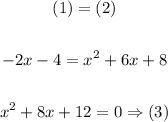
The solution to (3) is determined through a quadratic formula, the steps are as follows:

`\begin{gathered} \begin{equation*} x^2+8x+12=0 \end{equation*} \\ \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \\ \\ \\ a=1,b=8,c=12 \\ \\ x=(-(8)\pm√((8)_^2-4(1)(12)))/(2(1))=(-8\pm√(64-48))/(2) \\ \\ \text{ The solutions are:} \\ \\ x=(-8+√(16))/(2)=(-8+4)/(2)=(4)/(2)=-2\Rightarrow(i) \\ \\ x=(-8-√(64-48))/(2)=(-8-4)/(2)=-(12)/(2)=-6\Rightarrow(ii) \end{gathered}`

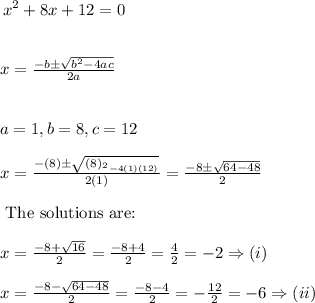
Therefore the values of the two functions at these two x values are as follows:

`\begin{gathered} y(-2)=-2(-2)-4=0 \\ \\ y(-6)=-2(-6)-4=8 \\ \\ -------------------------- \\ y(-2)=(-2)^2+6(-2)+8=4-12+8=0 \\ \\ y(-6)=(-6)^2+6(-6)+8=36-36+8=8 \\ \end{gathered}`

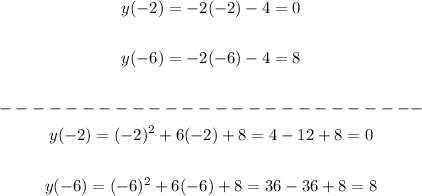
The two solutions therefore are:

`\begin{gathered} (x,y)=(-2,0)\Rightarrow\text{ Solution First} \\ \\ (x,y)=(-6,8)\Rightarrow\text{ Solution Second} \\ \end{gathered}`

The graph confirmation: