Question

A Sno-Cone at the carnival has the shape of a hemisphere on top of an inverted cone. What is the volume ofthe sno-cone if its radius is 5.2 cm and the height of the conical portion is 9.7 cm?

Answer 1

The Sno-Cone has two identifiable 3D figures, which are cone and hemisphere. Our key point here is to solve the volume of the cone and the hemisphere then add their volumes to solve for the total volume of the Sno-Cone.

The volume of the cone can be solved using the equation

`V_{\text{cone}}=r^2\pi(h)/(3)`

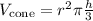
The radius of the sno-cone and its height are provided in the problem. Just substitute it on the equation above and compute, we get

The next thing to solve is the volume of the hemisphere. The volume of the hemisphere is half of the volume of a sphere, which is represented in the equation as

`V_{\text{hemisphere}}=((4)/(3)r^3\pi)/(2)=(2)/(3)r^3\pi`

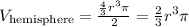
The radius of the cone is the same as the radius of the hemisphere. Substitute it on the equation above and compute, we get

`\begin{gathered} V_{\text{hemisphere}}=(2)/(3)(5.2cm)^3\pi \\ V_{\text{hemisphere}}=294.49cm^3 \end{gathered}`

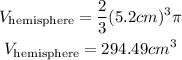
The overall volume of the sno-cone is the sum of the volume of the hemisphere and cone computed above.

`V_{\text{total}}=274.67+294.49=569.16cm^3`

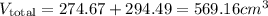
There