Question

Use the power reducing fabulous rewrite the identity in terms of the first power of cosine

Answer 1

The power reducing formula for the fourth power of the cosine function is:

`\cos ^4\theta=(3)/(8)+(1)/(2)\cos (2\theta)+(1)/(8)\cos (4\theta)`

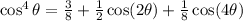
Replace θ=3x to find the expression for cos⁴(3x) in terms of the first power of the cosine function:

`\begin{gathered} \cos ^4(3x)=(3)/(8)+(1)/(2)\cos (2\cdot3x)+(1)/(8)\cos (4\cdot3x) \\ (3)/(8)+(1)/(2)\cos (6x)+(1)/(8)\cos (12x) \end{gathered}`

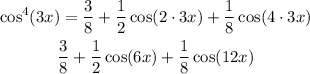
Therefore, the answer is:

`\cos ^4(3x)=(3)/(8)+(1)/(2)\cos (6x)+(1)/(8)\cos (12x)`

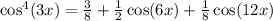
Use the second option to write this expression as input.