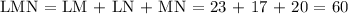LM = 23; MN = 20 ; QR = 34 ; Perimeter of LMN is 60
Here, we want to find the measures
From what we have, triangle LMN is formed by joining the midpoints of the triangle PQR
From the midpoint theorem, the sides of PQR are parallel and exactly half the measure of the sides they face
For example, LM is half PR
a) LM

b) MN
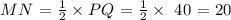
c) QR
Here, QR will be twice the measure of LN
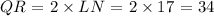
d) To find the perimeter of LMN, we have to add up the measure of the side lengths
We have this as;