Question

Find the standard deviation for the given data. Round your answer to one more decimal place than the original data. 223, 225, 300, 291, 289, 267, 171, 166, 141 A) 60.3 B) 28.8 C) 64.4 D) 56.8

Answer 1

The rule of the standard deviation of data is

`\sigma=\sqrt{(\sum_^(x-\mu)^2)/(n)}`

Where n is the number of data

μ is the mean

To find the mean sum of the data given and divide it by n

Since the given data are

`223,225,300,291,289,267,171,166,141`

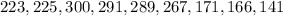
Then n = 9

`\begin{gathered} \mu=(223+225+300+291+289+267+171+166+141)/(9) \\ \\ \mu=(691)/(3) \end{gathered}`

Now, we will subtract the mean from each data, then ann the answers

`223-(691)/(3)=(-(22)/(3))^2=(484)/(9)`
`225-(691)/(3)=(-(16)/(3))^2=(356)/(9)`
`300-(691)/(3)=((209)/(3))^2=(43681)/(9)`
`291-(691)/(3)=((182)/(3))^2=(33124)/(9)`
`289-(691)/(3)=((176)/(3))^2=(30976)/(9)`
`267-(691)/(3)=((110)/(3))^2=(12100)/(9)`
`171-(691)/(3)=(-(178)/(3))^2=(31684)/(9)`
`166-(691)/(3)=(-(193)/(3))^2=(37249)/(9)`
`141-(691)/(3)=(-(268)/(3))^2=(71824)/(9)`

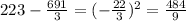
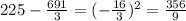
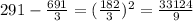
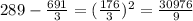
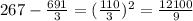
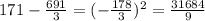
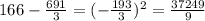
We will add all of these answers and divide them by n

`\begin{gathered} \sigma=\sqrt{((261478)/(9))/(9)} \\ \\ \sigma=56.8 \end{gathered}`

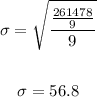
The answer is D