Question

Determine the number and type of solutions for the equation:-x^2-6x-9=0Is it: A. One repeated irrational number solutionB. Two different rational number solutionsC. Two different irrational number solutionsD. One repeated rational number solutionE. Two imaginary number solutions

Answer 1

The given equation is the quadratic equation:

`-x^2-6x-9=0`

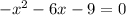
It is required to find the number and type of solutions.

To do this, the discriminant of the equation needs to be calculated.

Recall that the discriminant of a quadratic equation is:

`b^2-4ac`

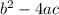
Where a is the coefficient of x², b is the coefficient of x, and c is the constant.

Recall also that:

• If the discriminant equals zero, the equation has one repeated rational number solution.

,

• If the discriminant is positive, the equation has two real solutions.

,

• If the discriminant is negative, the equation has two imaginary solutions.

,

• If the discriminant is a perfect square, then the equation has two real rational number solutions, it has two irrational number solutions.

Calculate the discriminant of the equation - x²- 6x - 9=0 by substituting a=-1, b=-6 and c=-9 into the discriminant formula:

`(-6)^2-4(-1)(-9)=36-36=0`

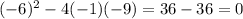
Since the discriminant equals zero, it follows that the equation has one repeated rational number solution.

The equation has one repeated rational number solution.

Option D is correct.