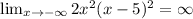Question

State the power function that the graph of f resembles for large values of x. Find the end-behavior for the function. Write your results using limit notation

Answer 1

Notice that:

`\begin{gathered} \lim _(x\rightarrow\infty)(2x^2(x-5)^2)/(x^4)=\lim _(x\rightarrow\infty)(2(x-5)^2)/(x^2) \\ =\lim _(x\rightarrow\infty)(2(x^2-10x+25))/(x^2) \\ =\lim _(x\rightarrow\infty)((2x^2)/(x^2)-(10x)/(x^2)+(25)/(x^2)) \\ =\lim _(x\rightarrow\infty)(2-(10)/(x)+(25)/(x^2)) \\ =\lim _(x\rightarrow\infty)2-\lim _(x\rightarrow\infty)(10)/(x)+\lim _(x\rightarrow\infty)(25)/(x^2) \\ =2-0+0 \\ =2 \end{gathered}`

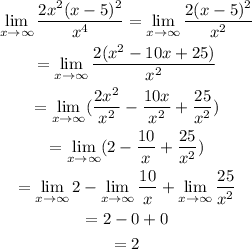
Which means that, for large values of x:

`2x^2(x-5)^2\approx2x^4`

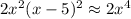
Since the function:

`f(x)=2x^4`

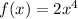
is a 4th degree monomial, with positive coefficient, then it keeps growing as x grows. Then, we know that:

`\lim _(x\rightarrow\infty)2x^2(x-5)^2=\infty`

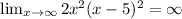
Which means that the end behavior is such that f(x) approaches infinity as x approaches infinity.

On the other hand, for large negative values of x, the function is also positive. Then:

`\lim _(x\rightarrow-\infty)2x^2(x-5)^2=\infty`