The limit of a function is the value that a function approaches as that function's inputs get closer and closer to some number.
The question asks us to estimate from the table:

To find the limit of g(x) as x tends to -2, we need to check the trend of the function as we head towards -2 from both negative and positive infinity.
From negative infinity, the closest value we can get to before -2 is -2.001 according to the values given in the table. The value of g(x) from the table is:
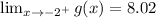
From positive infinity, the closest value we can get to before -2 is -1.999 according to the values given in the table. The value of g(x) from the table is:

From the options, the closest estimate for the limit is 8.03.
The correct option is the SECOND OPTION.