Question

A particle’s position along the x-axis is described by the functionx(t) = A t + B t2,where t is in seconds, x is in meters, and the constants A and B are given below.Randomized VariablesA = -4.9 m/sB = 6.9 m/s2q. Enter expression interms of A,B, t for the velocity of the particle as a function of time? What time will the velocity be zero?

Answer 1

Given,

The position function is, x(t)=At+bt²

A=-4.9 m/s

B=6.9 m/s²

The velocity is described as the rate of change if the displacement with time.

That is, the velocity is the time derivative of the displacement.

Therefore on differentiating the given function with respect to the time, we get the expression for the velocity.

i.e.,

`\begin{gathered} v(t)=(d(At+Bt^2))/(dt) \\ =A+2Bt \end{gathered}`

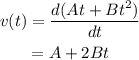
Therefore the expression for the velocity is A+2Bt

To know at what time the velocity will be zero,

`A+Bt=0`

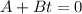
On simplifying the above equation,

`t=(-A)/(B)`

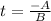
On substituting the known values in the above equation,

`t=\frac{-(-4.9\text{ )}}{6.9}=0.71\text{ s}`

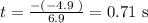
Therefore the velocity will be zero at 0.71 s