From the diagram provided, we have a right angled triangle with the hypotenuse (side facing the right angle) given as 55, while one of the other two sides is given as 44.
We shall apply the pythagoras' theorem as follows;
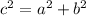
Where,
c = hypotenuse,
a and b = the other sides.
Therefore, we'll now have;
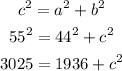
Next step, we'll subtract 1936 from both sides of the equation;
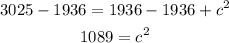
Add the square root sign to both sides of the equation;
![\begin{gathered} \sqrt[]{1089}=\sqrt[]{c^2} \\ 33=c \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2n99qi9gci3g32zwaf7ye7ef8lj9ivzor3.png)
ANSWER
Therefore, the correct answer is option C, that is 33 inches.