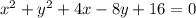The equation of a circle in center-radius form, is:

-Where the coordinates of the center of the circle are (h,k) and the radius of the circle is r.
From the given graph, we can see that the coordinates of the center are (-2,4) and the radius of the circle is 2.
a)
To determine the equation of the circle in center-radius form, replace h=-2, k=4 and r=2
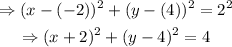
Therefore, the equation of the circle in center-radius form is:
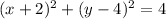
b)
To find the equation of the circle in general form, expand the parentheses and take all the terms to the left member:
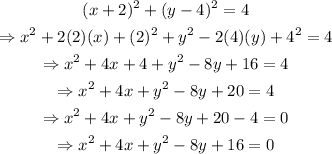
Write the quadratic terms first:
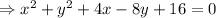
Therefore, the equation of the circle in general form, is: