Answer:
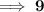
Explanation:
Given :
To Find :
- number of sides of a regular polygon, whose each exterior angle has a measure of 40°
Solution :
Since, the given polygon is a regular polygon.
It's each exterior angle is equal.
Sum of all the exterior angles = 360°
Number of exterior angles =
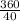 = 9°
= 9°
 Number of sides = 9
Number of sides = 9
Hence, it is nonagon.