How many real roots will this quadratic have? x² + 6x = -34 a. 1 real root b. 2 real roots c. 0 real roots or 2 complex/imaginary roots

Question

asked Dec 6, 2023 182k views

2 Answers

Rappongy · Answer 1 · 2023-12-08T08:37:40+0000

Answer:

Choice b: 2 real roots

Explanation:

The original equation is:
x² + 6x = -34

Adding 34 to both sides
x² + 6x + 34 = 0

This is a quadratic equation which can be solved by using the quadratic formula

The roots,
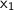$\sf x_1$ and
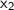$\sf x_2$ , of a quadratic equation of the form ax² + bx + c = 0 are given by:

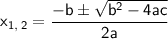
$\sf x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)$

In the equation given, a = 1, b = 6 and c = 34

So

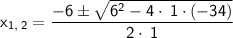
$\sf x_(1,\:2)=(-6\pm √(6^2-4\cdot \:1\cdot \left(-34\right)))/(2\cdot \:1)$

Let's first determine the square root term:

$\sf √(6^2-4\cdot \:1\cdot \left(-34\right))\\\\= √(6^2+136)\\\\=√(36+136)\\\\=√(172)\\\\$

Therefore the two roots are

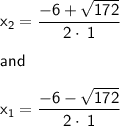
$\sf x_2=(-6+√(172))/(2\cdot \:1)\\\\and\\\\\sf x_1=(-6 - √(172))/(2\cdot \:1)$

Both these roots are real and different from each other. There is no need to compute.

Imaginary roots happen only when the term under the square root is negative

So answer is b: 2 real roots