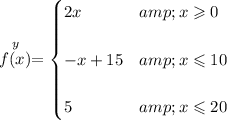Question

Please help!!! I really need this!!! It's piecewise functions......

Answer 1

well, let's take a peek at the graph, hmmm it has a straight line from the origin to (5,10), and then another straight line from (5,10) to (10,5) and then another one from there up to (20,5).

well, let's simply get the equations for each of those lines then

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{5}~,~\stackrel{y_2}{10}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{10}-\stackrel{y1}{0}}}{\underset{run} {\underset{x_2}{5}-\underset{x_1}{0}}} \implies 2 \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{2}(x-\stackrel{x_1}{0})\implies \boxed{y = 2x} \\\\[-0.35em] ~\dotfill`

`(\stackrel{x_1}{5}~,~\stackrel{y_1}{10})\qquad (\stackrel{x_2}{10}~,~\stackrel{y_2}{5}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{5}-\stackrel{y1}{10}}}{\underset{run} {\underset{x_2}{10}-\underset{x_1}{5}}} \implies \cfrac{ -5 }{ 5 }\implies -1`

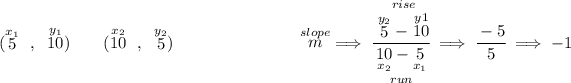
`\begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{10}=\stackrel{m}{-1}(x-\stackrel{x_1}{5}) \\\\\\ y-10=-x+5\implies \boxed{y=-x+15} \\\\[-0.35em] ~\dotfill`

`(\stackrel{x_1}{10}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{20}~,~\stackrel{y_2}{5}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{5}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{20}-\underset{x_1}{10}}} \implies \cfrac{ 0 }{ 10 }\implies 0 \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{0}(x-\stackrel{x_1}{10})\implies y-5=0\implies \boxed{y=5}`

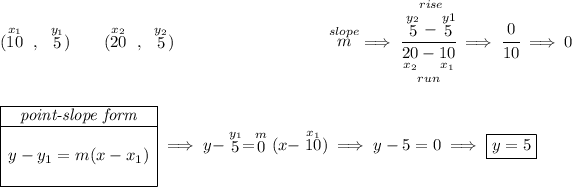
so then hmmm let's use those, we know how f(x) is moving now, so

`\stackrel{y}{f(x)}= \begin{cases} 2x&x\geqslant 0\\\\ -x+15&x\leqslant 10\\\\ 5&x\leqslant 20 \end{cases}`