Question

Find the zeros of the function. Enter the

solutions from least to greatest.
ƒ(x) = (x + 2)² – 16

Answer 1

x = - 6, x = 2

Explanation:

to find the zeros let f(x) = 0 , that is

(x + 2)² - 16 = 0 ( add 16 to both sides )

(x + 2)² = 16 ( take square root of both sides )

x + 2 = ±
`√(16)` = ± 4 ( subtract 2 from both sides )

x + 2 = - 2 ± 4

then

x = - 2 - 4 = - 6

x = - 2 + 4 = 2

Answer 2

-6, 2

Explanation:

So when finding the zeroes of function, you set it equal to zero:

`0 = (x+2)^2-16`

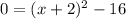
Add 16 to both sides

`16 = (x+2)^2`

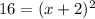
Take the square root of both sides:

`\pm4=x+2`

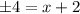
Subtract 2 from both sides

`\pm4-2=x`

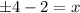
So to find the two solutions here, you take the positive and negative form of the 4

`-4 -2=x\\-6=x`

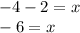
That's one solution, now take the positive value of 4

`4-2=x\\2=x`

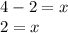
So now we have both of our solutions! We can also tell that we have all the solutions to the functions, because of the Fundamental Theorem of Algebra, which basically stats that any polynomial with degree n, will have exactly n solutions.

These n solutions, can be composed of complex and/or real solutions.