Question

The vertices of a quadrilateral are A(-1,6),B(-2,4),C(2,2), and D(3,4). Write a paragraph proof to determine whether quadrilateral ABCD is a rectangle. 15px

Answer 1

Answers will vary based on the method used, but the final slope-intercept form of the equation of A⁢B↔ will be the same.Let the equation of A⁢B↔ in slope-intercept form be y=m⁢x+d, where m is the slope and d is the y-intercept.The coordinates of points A and B are (1, 1) and (5, 3), respectively, so the slope of A⁢B↔ is m=yB−yAxB−xA=24=0.5.Substitute the value of m back in the equation:y = 0.5x + d.Substitute the coordinate of point A (1, 1) in the equation above, and solve for d: 1 = 0.5 + dd = 0.5.Therefore, the equation of A⁢B↔ is y = 0.5x + 0.5. To check whether C lies on A⁢B↔ substitute the x-coordinate of C into the right side of the equation: 0.5 (2.6) + 0.5 = 1.8.The result is equal to the y-coordinate of C. Thus, C satisfies the equation of A⁢B↔ which means that C lies on A⁢B↔.

Explanation:

I did it

Answer 2

Determining the slopes of each side, we get the slope of
`\overline{AB}` is
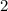`2`, the slope of
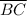`\overline{BC}` is -1/2, the slope of
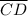`\overline{CD}` is 2, and the slope of
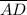`\overline{AD}` is -1/2. Since the slopes of sides AB and CD and BC and AD are equal, it follows that
`\overline{AB} \parallel \overline{CD}` and
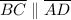`\overline{BC} \parallel \overline{AD}`. Thus, ABCD is a parallelogram because it is a quadrilateral with two pairs of opposite congruent sides. However, we can also note that the slope of side AB is the negative reciprocal of that of sides BC, and thus
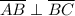`\overline{AB} \perp \overline{BC}`. Using the fact that perpendicular lines form right angles, we can conclude that
`\angle ABC` is a right angle, and since ABCD is thus a parallelogram with a right angle, it must also be a rectangle.