Answer:
(A) Alternate interior angles theorem
(B) Reflexive property
(C) Given
(D) SAS rule of congruency
(E) CPCTC
(F) If both pairs of opposite sides of a parallelogram are congruent, then the quadrilateral is a parallelogram
Explanation:
The two column proof required to prove that EFGH is a parallelogram is presented as follows;
Statement
 Reason
Reason
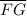 ║
║
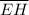
 Given
Given
∠FGE ≅ ∠HEG
 Alternate interior angles theorem
Alternate interior angles theorem
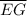 ≅
≅
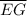
 Reflexive property
Reflexive property
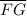 ≅
≅
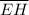
 Given
Given
ΔFEG ≅ ΔHEG
 SAS rule of congruency
SAS rule of congruency
 ≅
≅
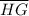
 CPCTC
CPCTC
EFGH is a parallelogram
 If both pairs of opposite sides of a parallelogram are congruent, then the quadrilateral is a parallelogram
If both pairs of opposite sides of a parallelogram are congruent, then the quadrilateral is a parallelogram
Where CPCTC stands for Congruent Parts of Congruent Triangles are Congruent