Question

1. An ant starts from the origin of a 2-D grid, at the point (0,0). Then each time it moves either i) right by one unit distance, e.g., from (0,0) to (1,0), ii) up by one unit distance, e.g., from (0,0) to (0,1), or iii) stay still, with probabilities 0.3, 0.2, and 0.5, respectively. After 10 moves, what is the probability that the ant ends up at point (2,5)

Answer 1

0.0091 = 0.91% probability that the ant ends up at point (2,5)

Explanation:

What is needed to move from the point (0,0) to the point (2,5) after 10 moves:

5 moves of up by 1 unit.

2 moves of right by 1 unit.

10 - (5 + 2) = 3 standing still.

Probability:

2 moves of right by 1 unit, each with 0.3 probability.

5 moves of up by 1 unit, each with 0.2 probability.

3 standing still, each with 0.5 probability.

Number of ways this can happen:

Arrangments of 10 moves, with 2, 5 and 3 repetitions. So

`T = (10!)/(2!5!3!) = 2520`

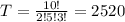
Probability:

`p = 2520*(0.3)^2*(0.2)^5*(0.5)^3 = 0.0091`

0.0091 = 0.91% probability that the ant ends up at point (2,5)