Answer:
 .
.
Explanation:
The goal is to rewrite
 in the vertex form
in the vertex form
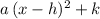 by completing the square (where
by completing the square (where
 ,
,
 , and
, and
 are constants.)
are constants.)
Expand the vertex form expression:
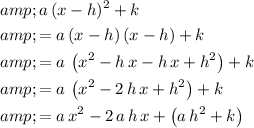 .
.
Compare this expression to
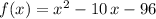 and solve for the constants
and solve for the constants
 ,
,
 , and
, and
 . Make sure that the coefficient of each term matches:
. Make sure that the coefficient of each term matches:
- Coefficient for the
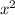 term:
term:
 in the expanded expression and
in the expanded expression and
 in the expression for
in the expression for
 . Hence,
. Hence,
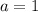 .
.
- Coefficient for the
 term:
term:
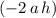 in the expanded expression and
in the expanded expression and
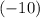 in the expression for
in the expression for
 . Hence,
. Hence,
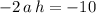 .
.
- Coefficient for the constant term:
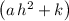 in the expanded expression and
in the expanded expression and
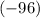 in the expression for
in the expression for
 . Hence,
. Hence,
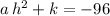 .
.
Substitute
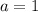 into the second equation,
into the second equation,
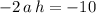 , and solve for
, and solve for
 .
.
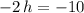 .
.
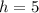 .
.
Substitute both
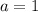 and
and
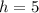 into the third equation,
into the third equation,
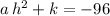 , and solve for
, and solve for
 .
.
 .
.
 .
.
Therefore,
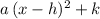 becomes
becomes
 .
.
Hence, the vertex form of the parabola
 would be:
would be:
 .
.