Answer:
The sample standard deviation is 13.22°F
Explanation:
Given - Often, frequency distributions are reported using unequal
class widths because the frequencies of some groups would
otherwise be small or very large. Consider the following data,
which represent the daytime household temperature the
thermostat is set to when someone is home for a random sample
of households. Determine the class midpoint, if necessary, for
each class and approximate the mean and standard deviation
temperature.
Temp Frequency Class Midpoint
61-64 34 63
65-67 68 66.5
68-69 196 69
70 191 70.5
71-72 122 72
73-76 81 75
77-80 52 79
To find - The sample standard deviation is _____degrees°F.
Proof -
Temp Frequency(f) Midpoint(m) m×f ( m - 70.73 )²×f
61-64 34 63 2142 2031.6
65-67 68 66.5 4522 1216.7
68-69 196 69 13524 586.6
70 191 70.5 13465.5 10.1
71-72 122 72 8784 196.8
73-76 81 75 6075 2224.4
77-80 52 79 4108 3556.4
∑f = 744 ∑m×f = 52620.5 ∑ = 9822.6
So, Mean =
 = 70.73
= 70.73
Sample standard deviation =
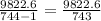 = 13.22
= 13.22
∴ we get
The sample standard deviation is 13.22°F