Question

Consider a large truck carrying a heavy load, such as steel beams. A significant hazard for the driver is that the load may slide forward, crushing the cab, if the truck stops suddenly in an accident or even in braking. Assume, for example, that a 10 000-kg load sits on the flatbed of a 20 000-kg truck moving at 12.0 m/s. Assume that the load is not tied down to the truck, but has a coefficient of friction of 0.500 with the flatbed of the truck.

A) Calculate the minimum stopping distance for which the load will not slide forward relative to the truck.
B) Is any piece of data unnecessary for the solution?
a) mass of the load.
b) mass of the truck.
c) velocity.
d) coefficient of static friction.
e) all are necessary.

Answer 1

A)

the minimum stopping distance for which the load will not slide forward relative to the truck is 14 m

B)

data that were not necessary to the solution are;

a) mass of truck and b) mass of load

Step-by-step explanation:

Given that;

mass of load
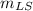`m_(LS)` = 10000 kg

mass of flat bed
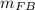`m_(FB)` = 20000 kg

initial speed of truck
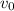`v_(0)` = 12 m/s

coefficient of friction between the load sits and flat bed μs = 0.5

A) the minimum stopping distance for which the load will not slide forward relative to the truck.

Now, using the expression

Fs,max = μs
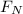`F_(N)` -------------let this be equation 1

where
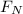`F_(N)` = normal force = mg

so

Fs,max = μs mg

ma
`_(max)` = μs mg

divide through by mass

a
`_(max)` = μs g ---------- let this be equation 2

in equation 2, we substitute in our values

a
`_(max)` = 0.5 × 9.8 m/s²

a
`_(max)` = 4.9 m/s²

now, from the third equation of motion

v² = u² + 2as

`v_(f)`² =
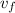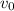`v_(0)`² + 2aΔx

where
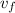`v_(f)` is final velocity ( 0 m/s )

a is acceleration( - 4.9 m/s² )

so we substitute

(0)² = (12 m/s)² + 2(- 4.9 m/s² )Δx

0 = 144 m²/s² - 9.8 m/s²Δx

9.8 m/s²Δx = 144 m²/s²

Δx = 144 m²/s² / 9.8 m/s²

Δx = 14 m

Therefore, the minimum stopping distance for which the load will not slide forward relative to the truck is 14 m

B) data that were not necessary to the solution are;

a) mass of truck and b) mass of load