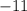Answer:
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Distributive Property
Algebra I
- Interval Notation
- Average Rate of Change:
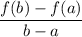
Explanation:
Step 1: Define
f(x) = -x² - 7x - 8
(1, 3) → a = 1, b = 3
Step 2: Find Average Rate
- Substitute in variables [Average Rate of Change]:
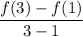
- [Change] Substitute in function:
![\displaystyle \displaystyle ([-(3)^2 - 7(3) - 8] - [-(1)^2 - 7(1) - 8])/(3 - 1)](https://img.qammunity.org/2022/formulas/mathematics/college/qdgcmor2dob71i3700dut9xh62u966hdlv.png)
- [Change] [Fraction] [Brackets] Evaluate exponents:
![\displaystyle \displaystyle ([-9 - 7(3) - 8] - [-1 - 7(1) - 8])/(3 - 1)](https://img.qammunity.org/2022/formulas/mathematics/college/sbnvnd4y87quj9pip6yu4ev27xvrafocdt.png)
- [Change] [Fraction] [Brackets] Multiply:
![\displaystyle \displaystyle ([-9 - 21 - 8] - [-1 - 7 - 8])/(3 - 1)](https://img.qammunity.org/2022/formulas/mathematics/college/3w9h8wzym66uhwsslg2mhsjadv9emgnks0.png)
- [Change] [Fraction] [Brackets] Subtract:
![\displaystyle \displaystyle ([-38] - [-16])/(2)](https://img.qammunity.org/2022/formulas/mathematics/college/qyiwoculf4wipjmpyk7ucykjmyy5tx6awm.png)
- [Change] [Fraction] [Distributive Property] Distribute negative:
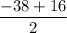
- [Change] [Fraction] Add:
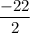
- [Change] [Fraction] Divide: