Answer:

Explanation:
To find the slope-intercept equation of the linear function represented by the table, we need to determine two things:
1. The slope
 of the line
of the line
2. The y-intercept

Step 1: Finding the Slope
The slope
 is calculated as the change in \( y \) divided by the change in
is calculated as the change in \( y \) divided by the change in
 :
:
![\[m = \frac{{\Delta y}}{{\Delta x}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/85df0kezoqgit2lxtk1v3auk8a9h9gfxdj.png)
We can pick any two points from the table to calculate the slope. Let's use the points
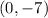 and
and
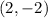 :
:
![\[m = \frac{{-2 - (-7)}}{{2 - 0}} = \frac{{5}}{2}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dva8bk2dpefinsb5z4shr5av82ztfn10pt.png)
Step 2: Finding the y-intercept
The y-intercept
 is the value of
is the value of
 when
when
 . According to the table, when
. According to the table, when
 .
.
Step 3: Writing the Equation
The slope-intercept form of a linear equation is
 .
.
Substituting the values we found for
 and
and
 , we get:
, we get:
![\[y = (5)/(2)x - 7\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ka1ettbxrlh70smejqqzmyxiefab2d9v7p.png)
So, the correct answer is
 .
.