Answer:
P(x < 2) = 0.4362 (4 d.p.)
Explanation:
To compute P(x < 2) for a binomial random variable with parameters n = 9 and p = 0.2, use the cumulative distribution function (CDF) of the binomial distribution.
P(x < 2) means the probability that x takes on a value less than 2. This can be calculated as:
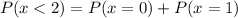
The binomial probability formula is:
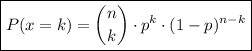
Calculate P(x = 0):
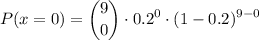

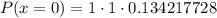
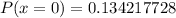
Calculate P(x = 1):
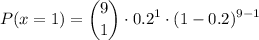
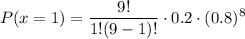

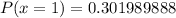
Now, add these probabilities together:
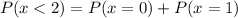

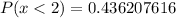
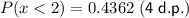
So, P(x < 2) for the given binomial random variable with n = 9 and p = 0.2 is approximately 0.4362 (rounded to four decimal places).