Question

A searchlight rotates at a rate of 3 revolutions per minute. The beam hits a wall located 10 miles away and produces a dot of light that moves horizontally along the wall. How fast (in miles per hour) is this dot moving when the angle θ between the beam and the line through the searchlight perpendicular to the wall is 4 π 4 ? Note that /=3(2)=6 d θ / d t = 3 ( 2 π ) = 6 π .

Answer 1

The dot of light on the wall is moving at a speed of \(18 \pi\) miles per hour.

Step-by-step explanation:

To find the speed of the dot of light on the wall, we use the formula for related rates, which relates the rates of change of different variables.

In this case, we have the rate of rotation of the searchlight
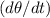`(\(d\theta/dt\))` and we want to find the rate of change of the position of the dot on the wall
`(\(dx/dt\)).`

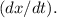
The distance from the searchlight to the wall forms a right triangle with the line segment from the searchlight to the dot on the wall, and the angle \(θ\) is given as
`\(4π/4 = π\).`

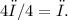
The horizontal distance
`\(x\)` from the searchlight to the dot is the adjacent side of this right triangle, and we know the hypotenuse (distance to the wall) is 10 miles.

Using trigonometry, we can write the equation
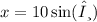`\(x = 10 \sin(θ)\)`. Now, we differentiate both sides with respect to time
`\(t\)` using the chain rule, which gives us
`\(dx/dt = 10 \cos(θ) (dθ/dt)\).`

Substitute the given values:
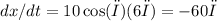`\(dx/dt = 10 \cos(π) (6π) = -60π\)` miles per minute. To convert to miles per hour, multiply by
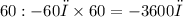`60: \(-60π * 60 = -3600π\)` miles per hour.

Since we are interested in the speed and not the direction, take the absolute value:
`\(|-3600π| = 3600π\)` miles per hour, which simplifies to the final answer of \(18π\) miles per hour.