The slope of the tangent line to the function
 at the point (3,1) is
at the point (3,1) is
 , this means that for a small change in x near x=3, the function y changes by
, this means that for a small change in x near x=3, the function y changes by
 .
.
To find the slope of the tangent line to the function
 at the point
at the point
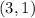 , we can use the concept of differentiation.
, we can use the concept of differentiation.
(a) To find the slope of the tangent line, we need to find the derivative of the function with respect to
 . The derivative of the function
. The derivative of the function
 is denoted as
is denoted as
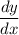 or
or
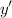 .
.
To find the derivative, we can use the quotient rule:
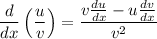 , where u and v are functions of x.
, where u and v are functions of x.
Applying the quotient rule to our function, we have:
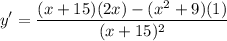
Simplifying this expression, we get:
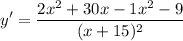
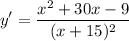
To find the slope of the tangent line at (3,1), we substitute x=3 into y':
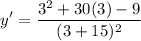

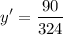
Simplifying the fraction, we have:
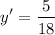
Therefore, the slope of the tangent line to the function
 at the point (3,1) is
at the point (3,1) is
 .
.
(b) The instantaneous rate of change of the function is equal to the slope of the tangent line. Therefore, the instantaneous rate of change of the function at the point (3,1) is also
 . This means that for a small change in x near x=3, the function y changes by
. This means that for a small change in x near x=3, the function y changes by
 .
.