Question

How much 5 m koh must be added to 1. 0 l of 0. 1 m glycine at ph 9. 0 to bring its ph to exactly 10. 0?.

Answer 1

The student's question relates to adjusting the pH of a glycine buffer by adding KOH. The Henderson-Hasselbalch equation is used to calculate pH changes in the buffer. However, specific details like the pKa of glycine are needed for precise calculations.

Step-by-step explanation:

The question pertains to the process of adjusting the pH of a glycine buffer solution by adding potassium hydroxide (KOH). Since the question involves buffer solutions, pH, and molarity, we need to use concepts from acid-base chemistry and buffer solution calculations. For a buffer solution that contains a weak acid (or a weak base) and its conjugate base (or acid), the pH can be calculated using the Henderson-Hasselbalch equation:

pH = pKa + log ([A-]/[HA])

where pKa is the acid dissociation constant, [A-] is the concentration of the conjugate base, and [HA] is the concentration of the weak acid. To adjust the pH, we would add KOH to the buffer, which would react with the weak acid component, increasing the ratio of [A-] to [HA] and thus raising the pH. However, the exact calculation of how much KOH must be added involves the buffer capacity and the change in pH, which requires specific details about the buffer composition, such as the pKa value. Without this information, the calculation cannot be completed.

In regards to the student's question on preparing a tris buffer, one would calculate the grams of tris needed using its molar mass and the desired molarity. Similarly, calculating the amount of HCl required to reach the desired pH involves knowing the pKa of tris and applying the Henderson-Hasselbalch equation.

Answer 2

Approximately 0.2851 liters or 285.1 ml of 5 M KOH needs to be added to achieve a pH of exactly 10.0 in the solution containing 1.0 L of 0.1 M glycine at pH 9.0.

To solve this problem, we'll use the Henderson-Hasselbalch equation, which relates the pH of a buffer solution to the pKa of the weak acid and the ratio of its conjugate base to weak acid. The equation is:

`\[ \text{pH} = \text{pKa} + \log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right) \]`

Given that glycine is a diprotic amino acid and has two dissociation constants (pKa values: 2.35 and 9.78 for its carboxyl and amino groups, respectively), we'll consider the second pKa value (9.78) since the pH is closer to this value.

At pH 9.0, the solution contains both the glycine and its conjugate base in a specific ratio. We want to increase the pH to 10.0 by adding a strong base (5 M KOH), which will react with glycine's acidic groups and convert them to their conjugate bases.

To achieve this change in pH, we'll calculate the change in concentration of the conjugate base needed, then use the amount of 5 M KOH required to achieve this change.

First, let's determine the ratio of the conjugate base
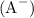`(\(\text{A}^-\))` to the weak acid
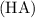`(\(\text{HA}\))` required to change the pH from 9.0 to 10.0 using the Henderson-Hasselbalch equation.

`\[\text{pH} = \text{pKa} + \log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right)\]`

`\[10.0 = 9.78 + \log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right)\]`

`\[\log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right) = 10.0 - 9.78 = 0.22\]`

`\[\frac{[\text{A}^-]}{[\text{HA}]} = 10^(0.22)\]`

`\[\frac{[\text{A}^-]}{[\text{HA}]} ≈ 1.584\]`

Now, let's determine the initial concentration of glycine
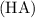`(\(\text{HA}\))` in the 1.0 L solution at pH 9.0 using its molarity (0.1 M) and the dissociation equation for glycine:

`\[\text{pH} = \text{pKa} + \log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right)\]`

`\[9.0 = 9.78 + \log\left(\frac{[\text{A}^-]}{0.1}\right)\]`

`\[\log\left(\frac{[\text{A}^-]}{0.1}\right) = 9.0 - 9.78 = -0.78\]`

`\[\frac{[\text{A}^-]}{0.1} = 10^(-0.78)\]`

`\([\text{A}^-] ≈ 0.1584 \, \text{M}\)`

Now, the change needed is the difference in the concentrations of
`\(\text{A}^-\)` at pH 10.0 and 9.0:

`\(\Delta[\text{A}^-] = [\text{A}^-]_{\text{final}} - [\text{A}^-]_{\text{initial}}\)`

`\(\Delta[\text{A}^-] = 1.584 \, \text{M} - 0.1584 \, \text{M}\)`

`\(\Delta[\text{A}^-] ≈ 1.4256 \, \text{M}\)`

Now, to find the volume of 5 M KOH needed to provide this amount of
`\(\text{A}^-\)`, we'll use the equation:

`\[M_1V_1 = M_2V_2\]`

Given that the concentration of KOH is 5 M:

`\[5 * V_{\text{KOH}} = 1.4256\]`

`\[V_{\text{KOH}} \approx 0.2851 \, \text{L}\]`