(a) Therefore, the change in the balloon's internal energy is
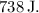
(b) Therefore, the change in temperature of the gas is approximately
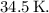
(a)To find the change in internal energy
 , you can use the first law of thermodynamics:
, you can use the first law of thermodynamics:
![\[\Delta U = Q - W\]](https://img.qammunity.org/2024/formulas/physics/high-school/xp6i86nillmkandwzz5fyvb79iso91iny0.png)
Where:
-
 = change in internal energy
= change in internal energy
- Q = heat added to the system
- W = work done by the system
Given:
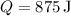 (heat absorbed by the gas)
(heat absorbed by the gas)
 (work done by the gas)
(work done by the gas)
![\[\Delta U = 875 \, \text{J} - 137 \, \text{J}\]](https://img.qammunity.org/2024/formulas/physics/high-school/vc68h334dgyheb70q80fq9u8c2bttjhyq6.png)
![\[\Delta U = 738 \, \text{J}\]](https://img.qammunity.org/2024/formulas/physics/high-school/9effjwp6issivjqvfiyx6g6y6g7uaor74m.png)
(b) To find the change in temperature
 of the gas, you can use the formula:
of the gas, you can use the formula:
![\[Q = nC_v\Delta T\]](https://img.qammunity.org/2024/formulas/physics/high-school/4jzauo337jdgya62p1l0zk9i618l3fjt06.png)
Where:
- n = number of moles of gas
-
 = molar specific heat at constant volume
= molar specific heat at constant volume
Given:
 of argon gas
of argon gas
For monatomic gases like argon,
 is the molar gas constant.
is the molar gas constant.
![\[\Delta T = (Q)/(nC_v)\]](https://img.qammunity.org/2024/formulas/physics/high-school/g3eovruq2z5xek286ibbgvdl50nsos9npn.png)
![\[\Delta T = \frac{875 \, \text{J}}{4.50 \, \text{mol} * (3)/(2)R}\]](https://img.qammunity.org/2024/formulas/physics/high-school/4mefhy3qzt05gk5766ky55sr53yfg1bymh.png)
The change in temperature can be calculated using the molar gas constant,
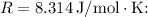
![\[\Delta T = \frac{875 \, \text{J}}{4.50 \, \text{mol} * (3)/(2) * 8.314 \, \text{J/mol}\cdot\text{K}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/qkgrt58ikvp2ymc1q73f72s3tgclm9bgjk.png)
![\[\Delta T \approx 34.5 \, \text{K}\]](https://img.qammunity.org/2024/formulas/physics/high-school/jhviznney54lg3w1ynn7bpxbdwlfctmrg6.png)