Answer:
Rectangles A & B: Proportional
Rectangles L & M: Not proportional
Explanation:
A proportional relationship between the corresponding sides of a pair of rectangles means that the ratios of the lengths of corresponding sides of the two rectangles are equal.

Rectangles A and B
In rectangle A, the length is 3 units and the width is 2 units.
In rectangle B, the length is 7.5 units and the width is 5 units.
To determine if there is a proportional relationship between the corresponding sides of the two rectangles, we compare the ratios of their lengths and widths.
- Ratio of lengths: A : B = 3 : 7.5
- Ratio of widths: A : B = 2 : 5
Set the ratios equal to each other:
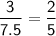
By cross-multiplying, we see that:
5 · 3 = 7.5 · 2
15 = 15
This demonstrates that there is a proportional relationship between the corresponding sides of rectangles A and B.

Rectangles L and M
In rectangle L, the length is 8 units and the width is 6 units.
In rectangle M, the length is 6 units and the width is 4 units.
To determine if there is a proportional relationship between the corresponding sides of the two rectangles, we compare the ratios of their lengths and widths.
- Ratio of lengths: L : M = 8 : 6
- Ratio of widths: L : M = 6 : 4
Set the ratios equal to each other:

By cross-multiplying, we see that:
4 · 8 = 6 · 6
32 = 36
Since 32 ≠ 36, it is evident that there is no proportional relationship between the corresponding sides of rectangles L and M.