Question

A box of books weighing 328 N moves with

a constant velocity across the floor when it is
pushed with a force of 378 N exerted downward at an angle of 25.6◦ below the horizontal.
Find µk between the box and the floor.

Answer 1

Approximately
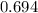`0.694`, assuming that the floor is level.

Step-by-step explanation:

Between two surfaces that are moving relative to one another, the coefficient of kinetic friction
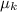`\mu_(k)` is equal to the ratio between friction and normal force.

Since the box in this question is moving at a constant speed, the box would be in a translational equilibrium. Forces on this box should be balanced in both the horizontal component and the vertical component.

The value of
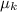`\mu_(k)` in this question can be found in the following steps:

• Decompose the external force into horizontal and vertical components.
• Balance forces in the horizontal direction to obtain an expression for the friction on this object.
• Balance forces in the vertical direction to find an expression for the normal force on this object.
• Divide the magnitude of friction by the magnitude of the normal force to find the coefficient of kinetic friction,
  `\mu_(k)`.

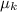At an angle of
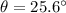`\theta = 25.6^(\circ)` from the horizontal, magnitude of the vertical and horizontal components of the external force would be:

• Horizontal component:
  `F\, \cos(\theta) = (378\; {\rm N})\, \cos(25.6^(\circ))`.
• Vertical component:
  `F\, \sin(\theta) = (378\; {\rm N})\, \sin(25.6^(\circ))`.

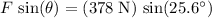Assume that the floor is level. Forces on this object in the horizontal direction would include:

• Horizontal component of the external force, pointing in the direction of motion.
• Friction from the ground, pointing backward opposite to the direction of motion.

Forces on this object are balanced in the horizontal direction. Hence, the magnitude of friction would be equal to that of the horizontal component of the external force:

`(\text{magnitude of friction}) = F\, \cos(\theta)`.

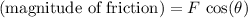Forces on this object in the vertical direction would include:

• Weight of this object, pointing downward.
• Vertical component of the external force, pointing downward.
• Normal force from the ground, pointing upward.

Forces on this object in the vertical direction are also balanced. The magnitude of the normal force (pointing upward) should be equal to the sum of the magnitude of the two forces pointing downward:

`\begin{aligned} & (\text{magnitude of normal force}) \\ =\; & (\text{magnitude of weight}) + F\, \sin(\theta)\end{aligned}`.

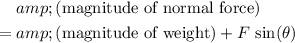It is given that the magnitude of the weight of this object is
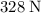`328\; {\rm N}`. To find the coefficient of kinetic friction, divide the magnitude of friction by the magnitude of the normal force:

`\begin{aligned}\mu_(k) &= \frac{(\text{magnitude of friction})}{(\text{magnitude of normal force})} \\ &= \frac{F\, \cos(\theta)}{(\text{magnitude of weight}) + F\, \sin(\theta)} \\ &= \frac{(378\; {\rm N})\, \cos(25.6^(\circ))}{(328\; {\rm N}) + (378\; {\rm N})\, \sin(25.6^(\circ))} \\ &\approx 0.694\end{aligned}`.