Question

HURP ME PLEASE!! PLEASE!! 100 POINTS

Answer 1

Explanation:

2x + 3 > 23. => x > 10.

x > 2 and x + 3 < 7. => 2 < x < 4.

When x = 5, x² + 2x = (5)² + 2(5) = 35.

When x = 5 and y = 3, 2x² + 2y = 2(5)² + 2(3) = 56.

Answer 2

See below:

Explanation:

Here is the solution to each of the given expressions with all steps:

a. 2x + 3 > 23

Subtract 3 from both sides:

2x + 3 - 3 > 23 - 3

2x > 20

Divide both sides by 2:

`\sf (2x)/(2)=(20)/(2)`

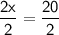
x > 10

Therefore, the solution to the inequality is x > 10.

`\hrulefill`

b. x > 2 and x + 3 < 7

Since we have two inequalities, we need to solve them separately and then combine the solutions.

Solving the first inequality:

x > 2

Solving the second inequality:

x + 3 < 7

Subtract 3 from both sides:

x + 3 - 3 < 7 - 3

x < 4

Now, we combine the solutions of the two inequalities:

x > 2 and x < 4

This means that the only values of x that satisfy both inequalities are the values that are greater than 2 but less than 4. The only such value is x = 3.

`\hrulefill`

c. [2x + 3] >= 23

The ceiling function, denoted by [], takes a real number as input and returns the smallest integer that is greater than or equal to the input.

Therefore, the expression [2x + 3] >= 23 means that the smallest integer that is greater than or equal to 2x + 3 must be greater than or equal to 23.

Solving the inequality:

2x + 3 >= 23

Subtract 3 from both sides:

2x + 3 - 3 >= 23 - 3

2x >= 20

Divide both sides by 2:

`\sf (2x)/(2)>=(20)/(2)`

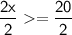
x >= 10

Therefore, the solution to the inequality is x >= 10.

`\hrulefill`

d. x² + 2x when x = 5**

Substitute x = 5 into the expression:

5² + 2 × 5

(25 + 10)

35

Therefore, the value of the expression when x = 5 is 35.

`\hrulefill`

e. 2x² + 2y when x=5,y=3

Substitute x = 5 and y = 3 into the expression:

2(5²) + 2(3)

2(25) + 2(3)

50 + 6

56

Therefore, the value of the expression when x = 5 and y = 3 is 56.