Question

Mason is getting quotes from two different landscaping companies to put river rock along one side of his house at a depth of 0.5 foot. The surface area of the space he wishes to install rock in is rectangular and has a length that is eight times its width. The first company charges $3.50 per cubic foot of rock and $80 for delivery. The second company charges $2.50 per cubic foot of rock and $120 for delivery Which system of equations can be used to determine the value of the width x at which the cost of the two companies, y, is the same?

Answer 1

the system of equations to determine the value of
`\( x \)` where the cost
`\( y \)` is the same for both companies is:

`\[ 14x^2 + 80 = y \]`

`\[ 10x^2 + 120 = y \]`

the two expressions for
`\( y \)` to find the value of
`\( x \)` where the costs are equal:

`\[ 14x^2 + 80 = 10x^2 + 120 \]`

To determine the value of the width
`\( x \)` at which the cost of the two companies
`\( y \)` is the same, we need to consider the volume of the river rock and the cost equations for both companies.

Let's define the variables:

-
`\( x \)` = width of the rectangular space in feet

-
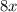`\( 8x \)` = length of the rectangular space in feet (since the length is eight times the width)

-
`\( 0.5 \)` = depth of the river rock in feet

The volume
`\( V \)` of the river rock needed for the space is given by the formula for the volume of a rectangular prism:

`\[ V = \text{length} * \text{width} * \text{depth} \]`

`\[ V = 8x * x * 0.5 \]`

`\[ V = 4x^2 \]`

Now, let's set up the cost equations for both companies:

For the first company:

`\[ y = 3.50V + 80 \]`

`\[ y = 3.50(4x^2) + 80 \]`

`\[ y = 14x^2 + 80 \]`

For the second company:

`\[ y = 2.50V + 120 \]`

`\[ y = 2.50(4x^2) + 120 \]`

`\[ y = 10x^2 + 120 \]`

Thus, the system of equations to determine the value of
`\( x \)` where the cost
`\( y \)` is the same for both companies is:

`\[ 14x^2 + 80 = y \]`

`\[ 10x^2 + 120 = y \]`

You can equate the two expressions for
`\( y \)` to find the value of
`\( x \)` where the costs are equal:

`\[ 14x^2 + 80 = 10x^2 + 120 \]`