Question

what size squares should office depot cut from each corner of the 24 inch cardboard so that the box will have maximum volume? what is the maximum volume

Answer 1

x = 4"

V max = 1024 sq inch

Explanation:

Let the length of the cut corner = x"

then, the length of the box = (24 - 2x)"

width of the box = (24 - 2x)"

height of the box = x"

Volume = length × width × height

= (24 - 2x)(24 - 2x)(x)

= (576 - 96x + 4x²)(x)

= 4x³ - 96x² + 576x

Volume max if the derivative = 0

`(dV)/(dx) =0`

`(3)(4x^((3-1)))-(2)(96x^((2-1)))+576x^((1-1))=0`

`12x^2-192x+576=0`

`x^(2) -16x+48=0`

`(x-4)(x-12)=0`

`x_1=4`

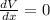
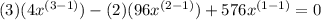
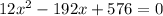
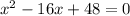
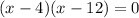
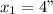
`x_2=12` (which is not available, because the length/width of the box = (24 - 2x)" → if x = 12" meaning length/width = 0)

∴ x = 4"

Volume = 4x³ - 96x² + 576x

Vol max = 4(4)³ - 96(4)² + 576(4)

= 1024 sq inch