It takes approximately
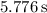 for the skier to come to a stop while sliding up the slope.
for the skier to come to a stop while sliding up the slope.
The skier is moving up a frictionless slope, meaning only the component of gravity parallel to the slope affects the skier's motion. The skier's initial velocity and the slope angle are given.
The acceleration due to gravity can be split into two components: one perpendicular to the slope (which doesn't affect the skier's motion) and one parallel to the slope.
The parallel component of gravity g can be calculated as
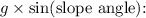
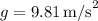 (acceleration due to gravity)
(acceleration due to gravity)
Slope angle =
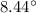
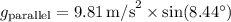
 (rounded to three decimal places)
(rounded to three decimal places)
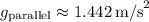
The skier is moving uphill, opposing the direction of the parallel component of gravity. To bring the skier to a stop, the acceleration he experiences will be his initial velocity
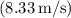 divided by the time (t) required to stop, assuming constant acceleration.
divided by the time (t) required to stop, assuming constant acceleration.
The kinematic equation used is:
![\[v = u + at\]](https://img.qammunity.org/2024/formulas/physics/high-school/utrncvx5x7bf1e71wocnr6wf89wf70qe0t.png)
Where:
v = final velocity (0 m/s, as the skier comes to a stop)
u = initial velocity (8.33 m/s)
a = acceleration

t = time taken to stop
Rearranging the equation to solve for time:
![\[t = (v - u)/(a)\]](https://img.qammunity.org/2024/formulas/physics/high-school/o5ilveg4t37eoa0u80hkomp4pvp4k2mlbl.png)
![\[t = (0 - 8.33)/(-1.442)\]](https://img.qammunity.org/2024/formulas/physics/high-school/lbpjd2yldqdh5qvoizkrre7eetvvnwqdo6.png)
![\[t \approx (-8.33)/(-1.442)\]](https://img.qammunity.org/2024/formulas/physics/high-school/wf51fhf0u81ikbctbroxvigapo6qgbv7pb.png)
![\[t \approx 5.776 \, \text{s}\]](https://img.qammunity.org/2024/formulas/physics/high-school/vbf48f67e0lxvr0ophj97d1pjg2ob92mkp.png)
Question:
A skier is moving
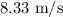 when he starts to slide UP a
when he starts to slide UP a
 frictionless slope. How much time does it take him to come to a stop?
frictionless slope. How much time does it take him to come to a stop?
(Unlt = s)