Question

Find the 12th term of the geometric sequence 10, -50, 250, ...10,−50,250,...

Answer 1

12th term = 488,281,250

Explanation:

The formula for the nth term of a geometric sequence is given by:

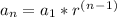`a_(n)=a_(1)*r^(^n^-^1^)`, where

• a1 represents the first term (10 in this case),
• r represents the common ratio,
• and n represents the term position (e.g., 1st, 12th, etc.)

Finding the common ratio:

• The common ratio is the quotient of two consecutive term.

This means that we can find the common ratio by dividing -50 by 10:

`r=-50/10\\\\r=-5`

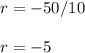
Thus, the common ratio is -5.

Finding the 12th term:

Now we can find the 12th term by substituting 10 for a1, -5 for r, and 12 for n in the geometric sequence nth term formula:

`a_(12)=10(-5)^(^1^2^-^1^)\\ \\a_(12)=10(-5)^(^1^1^)\\ \\a_(12)=10(-48828125)\\ \\a_(12)=-488281250`

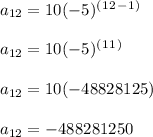
Thus, -488,281,250 is the 12th term of the geometric sequence.