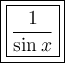Question

Simplify (cosx/sinx) +(sinx/1+cosx) and express answer in terms of sinx

Answer 1

`\cfrac{\cos(x)}{\sin(x)}+\cfrac{\sin(x)}{1+\cos(x)}\implies \cfrac{\cos(x)[1+\cos(x)]~~ + ~~\sin(x)\sin(x)}{\underset{\textit{using this LCD}}{\sin(x)[1+\cos(x)]}} \\\\\\ \cfrac{\cos(x)+\cos^2(x)~~ + ~~\sin^2(x)}{\sin(x)[1+\cos(x)]}\implies \cfrac{\cos(x)~~ + ~~1}{\sin(x)[1+\cos(x)]} \\\\\\ \cfrac{1+\cos(x)}{\sin(x)[1+\cos(x)]}\implies \boxed{\cfrac{1}{\sin(x)}}\implies \csc(x)`

Answer 2

`(1)/(\sin x)`

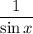
Explanation:

Given trigonometric expression:

`(\cos x)/(\sin x)+(\sin x)/(1+\cos x)`

To simplify the given expression in terms of sin x, begin by making the denominators of the two fractions the same. The common denominator is sin x(1 + cos x). Therefore, multiply the numerator and denominator of the first fraction by (1 + cos x), and numerator and denominator of the second fraction by sin x:

`(\cos x)/(\sin x)\cdot (1+\cos x)/(1+\cos x)+(\sin x)/(1+\cos x)\cdot (\sin x)/(\sin x)`

`(\cos x(1+\cos x))/(\sin x(1+\cos x))+(\sin^2x)/(\sin x(1+\cos x))`

Now we have a common denominator for both fractions, we can add the fractions:

`(\cos x(1+\cos x)+\sin^2x)/(\sin x(1+\cos x))`

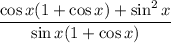
Simplify the numerator by expanding the brackets:

`(\cos x+\cos^2 x+\sin^2x)/(\sin x(1+\cos x))`

Apply the trigonometric identity sin²x + cos²x = 1 to the numerator:

`(\cos x+1)/(\sin x(1+\cos x))`

`(1+\cos x)/(\sin x(1+\cos x))`

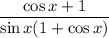
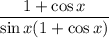
Cancel the common factor (1 + cos x):

`(1)/(\sin x)`

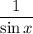
Therefore, the simplified trigonometric expression expressed in terms of sin x is:

`\large\boxed{\boxed{(1)/(\sin x)}}`