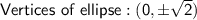Question

Identify the vertices and foci of the ellipse.

9x^2+y^2=18

Answer 1

`\sf \textsf{ Vertices of ellipse} :(0,\pm √(2))`

`\sf \textsf{Foci of ellipse} : ( 0, \pm 4 )`

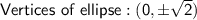
Explanation:

Definition:

The vertices of an ellipse are the two points that are the farthest away from the center of the ellipse.

The foci of an ellipse are two points that are located on its major axis, and are the same distance away from the center of the ellipse.

Formula:

The vertices and foci of an ellipse can be found using the following formulas:When b is greater than a.

• Vertices: (h , k ± b)
• Foci: (h, k ± c)

where:

• h and k are the center of the ellipse
• a is the semi-major axis
• c is the semi-minor axis

Solution:

In order to find the vertices and foci of the ellipse 9x² + y² = 18, we first need to rewrite the equation in standard form. The standard equation of the ellipse is given by:

`\sf ((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

Now, we find rewrite kmthe equation in standard form by dividing both sides by 18, we get

`\sf (9x^2)/(18)+(y^2)/(18)=(18)/(18)`

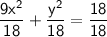
Comparing with this equation, we get

`\sf ((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

`\sf a^2 = 2`

`\sf a =√(2)`

`\sf b^2 = 18`

`\sf b =√(18)= 3√(2)`

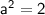
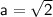
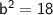
Center: (0, 0)

Now, Find the vertices:

`\sf Vertices: (0,0 \pm √(2))`

`\sf Vertices: (0,\pm √(2))`

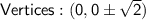
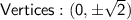
Find the foci:

`\sf Foci: (0, 0\pm c)`

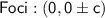
The linear eccentricity (focal distance) (c) can be calculated by the following formula:

`\sf c^2 = b^2 - a^2`

`\sf c^2 =( 3√(2))^2 - (√(2))^2`

`\sf c^2 = 18 - 2`

`\sf c^2 = 16`

`\sf c =√(16)`

`\sf c = \pm 4`

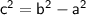
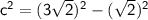
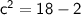
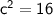
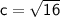
So,

`\sf Foci: ( 0, \pm 4 )`

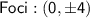
Therefore,

`\sf \textsf{ Vertices of ellipse} :(0,\pm √(2))`

`\sf \textsf{Foci of ellipse} : ( 0, \pm 4 )`