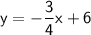Answer:
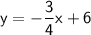
Explanation:
The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept.
We know that the slope of the line is -3/4, and we know that the line passes through the point (8,0).
We can use this information to find the y-intercept, b.
Substituting the known values into the slope-intercept form gives us:


Isolate b, we get
 ```
```
Therefore, the equation of the line in slope-intercept form is: