Answer:
a > -2n - 14
Explanation:
In order to solve the inequality 15 - 4(n + 7) < 2a + 17 for a, we can follow these steps:
Distribute the -4 in the left-hand side:
15 - 4(n + 7) < 2a + 17
15 - 4n - 28 < 2a + 17
Combine the constant terms on the right-hand side:
-4n - 13 < 2a + 17
Subtract 17 in both sides:
-4n - 13 - 17 < 2a + 17 - 17
2a > - 4n - 30
Divide both sides by 2:
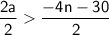
a > - 2n - 14
Since a can be any number greater than -15 - 2n, the solution to the inequality is:
a > -2n - 14
Note: This is the most general solution to the inequality. If we have any specific values for n, we can substitute them into the inequality to get a more specific solution.